Firebird Internal CTF 2023 Writeup

Like in 2021 and 2022, I contributed some challenges for Firebird’s internal CTF, which are from the Hong Kong University of Science and Technology. This time I wrote three crypto challenges: Randomsum, Shelter and Threerider.

There were 24 teams participating. There were three solves for Randomsum, while Shelter and Threerider were unsolved during the CTF.

Randomsum

Challenge Summary

I am leaking random bits of the RSA factors. Who doesn’t like leaks?

Attachment: chall.py • output.txt

We are given a 2048-bit RSA modulus $n$ , a public exponent $e = 65537$ and an encrypted flag $c$ . We are also given $t$ , which consists of 2048 bits (1318 distinct bits) from the factors, $p$ and $q$ . The objective is to recover the flag.

from Crypto.PublicKey import RSA
import random

random.seed(1337)

key = RSA.generate(2048)

t = [(key.p>>random.getrandbits(10))&1 if random.getrandbits(1) else (key.q>>random.getrandbits(10))&1 for i in range(2048)]
t = sum(t[i]<<i for i in range(2048))

with open('flag.txt', 'rb') as f:
    m = int.from_bytes(f.read(), 'big')

n, e = key.n, key.e
c = pow(m, e, n)

print(f'{n = }')
print(f'{e = }')
print(f'{t = }')
print(f'{c = }')

# n = 23972924803656725645946104612288180239254366533835447570211958435888835149024704127730216635918366064642338427956144263722073485986182242950506562077115261972266819566896991605805331175926336936623727858956342095970617971414648408199255433214266089182676417304576439449775708611349397255997892478936263800821533938404508818638694040349742659681140030800595271768949111564030020912493782604042297523251856213731597666043107228963973074577037344345426025975807448211052650699923918471883180836394144595630503970610793789138051476548955355193194759840128264687246565426588680843522246453634852078525991710060236523993541
# e = 65537
# t = 14000066433047292246448752794201977165563733655047203575867121262166187560566711892325594792129845153282249633931642143973215540568376319171334159461972160877466256238242152503653373908684017280676080125004854850332445723153614845802146395899581463896936557611606222767193353523987995818833578861773617167644193038121558267674251210114195760011821306729346761634659759967871454608623374306270379642305886119902085577927092579512468263725679201030921437666386689058685094677660425920780030296995254804923997961573399239884517270135267952236745232513979074599714453057660939074051865674834210296195715452442772175320306
# c = 6629119219609628910262885521069144816410786299451464969111007624958603576922839074850618464009859754669933262329186876226112761547177882680972685257697161919090897947135355903504454390331332951864051787079151186147963687429869735814443602986151345233136170388603746969296411646714158233418888611277576374237710204734229716394950713361265013458346462648487382316305877942127752214474859094795859454295294490880154326380500685914654596927550241665243599892940472157748432105831205326132442653659482947911799058715375236555903827420335782334212566356002880715361572706447898027515949713485430213701388248011598192532689

Solution

Since we are given $t$ (i.e., 1318 distinct bits of $p$ and $q$ ), we can immediately apply from section 4.3.1¹ to factorize $n$ . In short, $p$ and $q$ can be obtained with branch-and-prune algorithm by checking $n\ \text{mod}\ 2$ , $n\ \text{mod}\ 2^2$ and so on.

? Alternate solution. Mushroom1 used z3 to recover

p

and

q

. I am surprised that the challenge can be solved with z3.

Solution script

import random
import sys

MASKS = [(2<<i)-1 for i in range(1024)]

def guess(n, _ps, _qs, p0=0, q0=0, bits=0):
    n0 = p0 * q0
    if n == n0: return p0
    if n < n0: return

    for pb in _ps[bits]:
        p1 = p0 | (pb<<bits)
        for qb in _qs[bits]:
            q1 = q0 | (qb<<bits)
            if p1*q1 & MASKS[bits] != n & MASKS[bits]: continue
            res = guess(n, _ps, _qs, p1, q1, bits+1)
            if res is not None: return res

sys.setrecursionlimit(1027)
n = 23972924803656725645946104612288180239254366533835447570211958435888835149024704127730216635918366064642338427956144263722073485986182242950506562077115261972266819566896991605805331175926336936623727858956342095970617971414648408199255433214266089182676417304576439449775708611349397255997892478936263800821533938404508818638694040349742659681140030800595271768949111564030020912493782604042297523251856213731597666043107228963973074577037344345426025975807448211052650699923918471883180836394144595630503970610793789138051476548955355193194759840128264687246565426588680843522246453634852078525991710060236523993541
e = 65537
t = 14000066433047292246448752794201977165563733655047203575867121262166187560566711892325594792129845153282249633931642143973215540568376319171334159461972160877466256238242152503653373908684017280676080125004854850332445723153614845802146395899581463896936557611606222767193353523987995818833578861773617167644193038121558267674251210114195760011821306729346761634659759967871454608623374306270379642305886119902085577927092579512468263725679201030921437666386689058685094677660425920780030296995254804923997961573399239884517270135267952236745232513979074599714453057660939074051865674834210296195715452442772175320306
c = 6629119219609628910262885521069144816410786299451464969111007624958603576922839074850618464009859754669933262329186876226112761547177882680972685257697161919090897947135355903504454390331332951864051787079151186147963687429869735814443602986151345233136170388603746969296411646714158233418888611277576374237710204734229716394950713361265013458346462648487382316305877942127752214474859094795859454295294490880154326380500685914654596927550241665243599892940472157748432105831205326132442653659482947911799058715375236555903827420335782334212566356002880715361572706447898027515949713485430213701388248011598192532689

# Known bits
random.seed(1337)
bs = [(0, random.getrandbits(10)) if random.getrandbits(1) else (1, random.getrandbits(10)) for i in range(2048)]

_ps = [[0, 1] for _ in range(1024)]
_qs = [[0, 1] for _ in range(1024)]

for i, (id, b) in enumerate(bs):
    v = (t>>i) & 1
    if id == 0:
        assert _ps[b] in [[v], [0, 1]]
        _ps[b] = [v]
    else:
        assert _qs[b] in [[v], [0, 1]]
        _qs[b] = [v]

p = guess(n, _ps, _qs)
assert n % p == 0
q = n // p

phi_n = (p-1) * (q-1)
d = pow(e, -1, phi_n)

m = pow(c, d, n)
flag = int(m).to_bytes(2048//8, 'big').lstrip(b'\0')
print(f'{flag = }')

Shelter

Challenge Summary

I hope my account is intact under the hackers’ attack!

nc HOST PORT

Attachment: chall.py • auth.py • hacker.py

We are given an authentication service which allows us to

[register] create a new user with a given username and password,
[sign in] sign in to a user with a set of credentials by returning a token,
[auth] retrieve the username from the token.

Remarkably, the token is a ciphertext of username=[USERMAME]&password=[PASSWORD], using AES-CBC with a fixed key and a random IV. It is notable that the auth endpoint is vulnerable to the padding oracle attack.

On the other hand, we are also given a hacker’s exploit which attempts to steal the username and password from a given token. The goal is to create a valid token such that the hacker is unable to retrieve its credentials with the crack function.

class Hacker:
    def __init__(self, srv):
        # The function to check if the padding is correct
        self.srv = srv

    def __oracle(self, token):
        try:
            self.srv.authenticate(token.hex())
            return True
        except Exception as err:
            return str(err) not in [
                'Padding is incorrect.',
                'PKCS#7 padding is incorrect.'
            ]


    def __recover_block(self, ciphertext_block):
        iv = bytearray(16)

        for k in range(16):
            for i in range(256):
                iv[15-k] = i
                crafted_iv = xor(iv, bytes([k+1 for _ in range(16)]))
                if self.__oracle(crafted_iv + ciphertext_block): break
        return iv

    def __recover(self, ciphertext):
        return b''.join([
            xor(ciphertext[i-16:i],
                self.__recover_block(ciphertext[i:i+16]))
            for i in range(16, len(ciphertext), 16)
        ])
    
    def crack(self, token):
        token = bytes.fromhex(token)
        m = self.__recover(token)
        m = unpad(m, 16)
        m = parse_qs(m.decode())

        username, = m.get('username')
        password, = m.get('password')

        return username, password

Solution

The padding oracle and its attacks

Suppose that we are given a function $\mathcal{O}$ that tells us whether a ciphertext $c$ has a valid PKCS#7 padding, i.e.,

$\mathcal{O}(c) = \begin{cases} \color{green}{\checkmark} & \text{if}\ c\ \text{has a valid padding} \\ \color{red}{✗} & \text{otherwise} \end{cases}.$

There are a lot of instances vulnerable to the padding oracle attack. It affected multiple frameworks like Ruby on Rails², ASP.NET and so on.

Let’s get to the details of the padding oracle attack, which happens in the cipher block chaining (CBC) mod of operation. If we let $m_1$ , $c_0$ and $c_1$ being respectively a plaintext, an IV and a ciphertext (all of them are 16-byte long), then the below relation holds:

$m_1 = c_0 \oplus \text{Decrypt}_k(c_1).$

The general idea for the padding oracle attack is to change $c_0$ and keep $c_1$ fixed. We can recover $\text{Decrypt}_k(c_1)$ by checking whether $m_1$ has a valid padding. For example, we want to recover the below ciphertext:

000102030405060708090a0b0c0d0e0f 1d53a4e415b0893fc386fbea776b7198

Assuming that the ciphertext decrypts to 68656c6c6f20776f726c642104040404. Passing the ciphertext to $\mathcal{O}$ would return $\color{green}{\checkmark}$ because it has a valid padding (the message ends with four 04s).

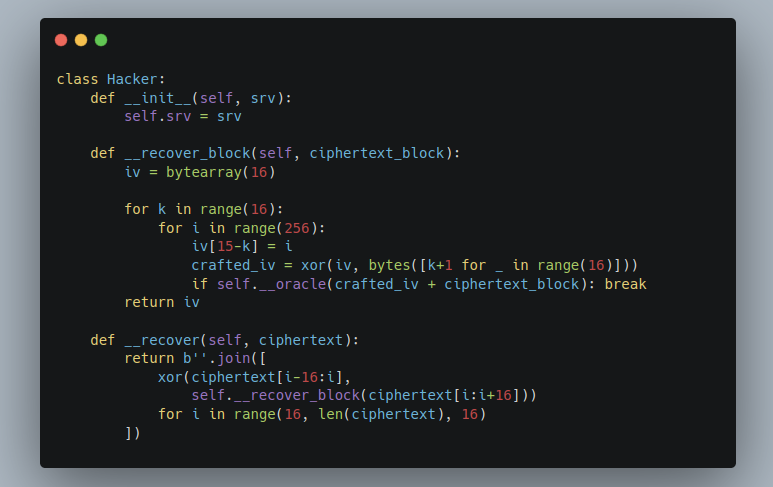
Of course, as the hacker we do not have the access to the plaintext. We have to use $\mathcal{O}$ to recover the plaintext byte-by-byte. Let’s follow the algorithm given from __recover_block and see how $\mathcal{O}$ recovers the plaintext. To begin, it sets

$\begin{aligned} & c_0 = \texttt{01010101010101010101010101010101} \quad \text{and} \\ & c_1 = \texttt{1d53a4e415b0893fc386fbea776b7198}. \end{aligned}$

? Why $\texttt{0101…0101}$ ? I think it is more elegant to define

c_0

with

\hat{c_0}

and the padding.

\hat{c_0}

is a counter and it would eventually be

\text{Decrypt}_k(c_1)

, and is initially defined to be

\texttt{0000…0000}

. On the other hand, when we are recovering the last character of

\text{Decrypt}_k(c_1)

, we make the padding to be

\texttt{0101…0101}

(which will be changed to

\texttt{0202…0202}

\texttt{0303…0303}

when we try to recover the second last character onwards)… In short, the code to recover

\text{Decrypt}_k(c_1)

(thus

m_1

) will look prettier.

The ciphertext decrypts to 69656f6e6a2470697b646f2b09080b0a, and it does not have a valid padding, i.e., $\mathcal{O}(c_0 \ || \ c_1) = \color{red}{✗}$ . We then send $\mathcal{O}(c_0′ \ || \ c_1)$ , where

$\begin{aligned} c_0′ &= \texttt{00000000000000000000000000000001} \oplus \texttt{01010101010101010101010101010101} \\ &= \texttt{01010101010101010101010101010100}. \end{aligned}$

The corresponding plaintext is 69656f6e6a2470697b646f2b09080b0b, which also imply that $\mathcal{O}(c_0′ \ || \ c_1) = \color{red}{✗}$ . The below figure shows the results of the 256 possible attempts:

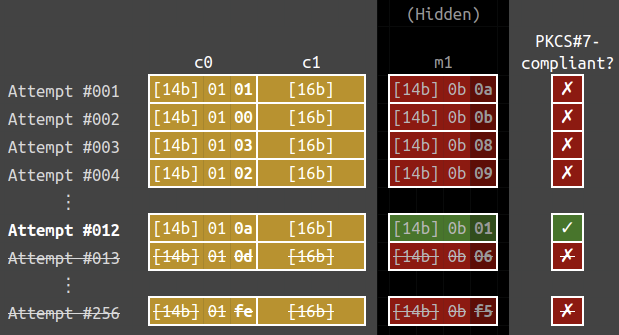
Firebird Internal CTF 2023 Writeup — The 256 attempts to recover the last byte of $m_1$ .

Eventually, we will send $\mathcal{O}(c_0” \ || \ c_1)$ with

$\begin{aligned} c_0” &= \texttt{0000000000000000000000000000000b} \oplus \texttt{01010101010101010101010101010101} \\ &= \texttt{0101010101010101010101010101010a}. \end{aligned}$

The plaintext is now 69656f6e6a2470697b646f2b09080b01 and it has a valid PKCS#7 padding, i.e., $\mathcal{O}(c_0” \ || \ c_1) = \color{green}{\checkmark}$ . Knowing this as a valid plaintext, we immediately know that the last byte of the plaintext (denoted by $m_1”$ ) is a 01. Therefore, we know that the last byte of $\text{Decrypt}_k(c_1)$ is $\texttt{0a} \oplus \texttt{01} = \texttt{0b}$ , using the relation

$\begin{aligned} & m_1” = c_0” \oplus \text{Decrypt}_k(c_1) \\ \Longrightarrow \quad & \texttt{{\color{gray}[15 bytes]}01} = \texttt{{\color{gray}[15 bytes]}0a} \oplus \text{Decrypt}_k(c_1) \\ \Longrightarrow \quad & \text{Decrypt}_k(c_1) = \texttt{{\color{gray}[15 bytes]}01} \oplus \texttt{{\color{gray}[15 bytes]}0a} = \texttt{{\color{gray}[15 bytes]}0b}. \end{aligned}$

Subsequently, we can recover the second last byte. Define $c_0^{(3)}$ by

$\begin{aligned} c_0^{(3)} &= \texttt{0000000000000000000000000000000b} \oplus \texttt{02020202020202020202020202020202} \\ &= \texttt{02020202020202020202020202020209}. \end{aligned}$

The plaintext for $c_0^{(3)} \ || \ c_1$ is 6a666c6d6927736a78676c280a0b0802, thus $\mathcal{O}(c_0^{(3)} \ || \ c_1) = \color{red}{✗}$ . We can keep increasing the counter for the second-last byte. Eventually, the counter will be increased to $\texttt{0a}$ … and this is its corresponding $c_0^{(4)}$ :

$\begin{aligned} c_0^{(4)} &= \texttt{00000000000000000000000000000a0b} \oplus \texttt{02020202020202020202020202020202} \\ &= \texttt{02020202020202020202020202020809}. \end{aligned}$

The plaintext for $c_0^{(4)} \ || \ c_1$ is 6a666c6d6927736a78676c280a0b0202, thus $\mathcal{O}(c_0^{(4)} \ || \ c_1) = \color{green}{\checkmark}$ . Thus the last two bytes of $\text{Decrypt}_k(c_1)$ is $\texttt{0a0b}$ , since

$\begin{aligned} & m_1^{(4)} = c_0^{(4)} \oplus \text{Decrypt}_k(c_1) \\ \Longrightarrow \quad & \texttt{{\color{gray}[14 bytes]}0202} = \texttt{{\color{gray}[14 bytes]}0a0b} \oplus \text{Decrypt}_k(c_1) \\ \Longrightarrow \quad & \text{Decrypt}_k(c_1) = \texttt{{\color{gray}[14 bytes]}0202} \oplus \texttt{{\color{gray}[14 bytes]}0809} = \texttt{{\color{gray}[14 bytes]}0a0b}. \end{aligned}$

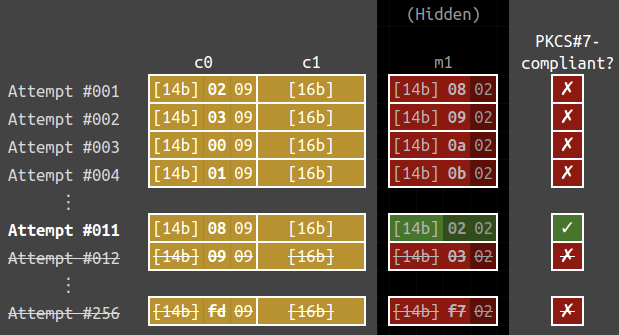
We can repeat the process to recover $\text{Decrypt}_k(c_1)$ . With that, we can easily obtain $m_1$ by the identity we mentioned at the very beginning:

$m_1 = c_0 \oplus \text{Decrypt}_k(c_1).$

By the way, since we will be getting the error message from the auth endpoint, it could tell us if the padding is correct. With that said, this endpoint has a padding oracle and thus cannot escape from the padding oracle vulnerability.

> auth 204094b9bec1ea6b9473d345130699d2de1c31278bda8b9f4695bc8fac7116735f78bb7509cd5add82abcdca9bf7989d 
?️ The token is correct for foo!
> auth 204094b9bec1ea6b9473d345130699d2de1c31278bda8b9f4695bc8fac7116735f78bb7509cd5add82abcdca9bf7989e 
?️ Invalid token: Padding is incorrect..

A corner case

I was not entirely correct in the previous section. When recovering the last byte, the trailing byte may not be 01 for the padding to be PKCS#7-compliant. Instead, it could end with 0202 (or 030303, 04040404, …).

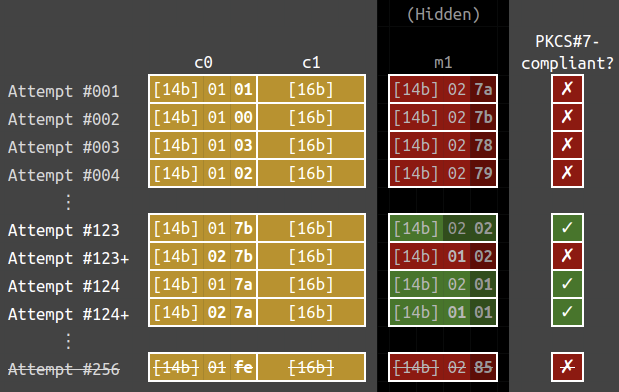
For instance, let’s look at the case $m_1 = \texttt{{\color{gray}[14 bytes]}0201}$ and $c_0 = \texttt{{\color{gray}[14 bytes]}017a}$ . The below are the 256 oracle calls that recovers the last byte of $m_1$ . Note that $c_1$ below is kept constant in the attempts.

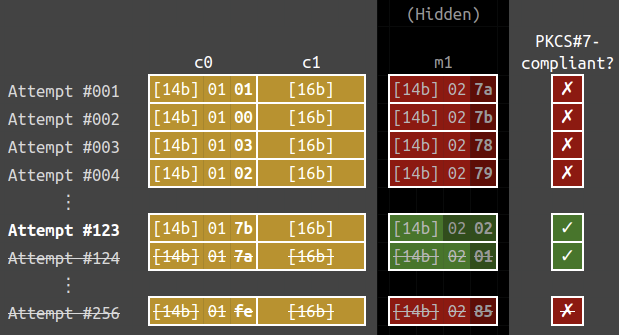
We can see that attempts #123 and #124 have valid paddings, i.e.,

$\mathcal{O}(\texttt{{\color{gray}[14 bytes]}017b{\color{gray}[16 bytes]}}) = \mathcal{O}(\texttt{{\color{gray}[14 bytes]}017a{\color{gray}[16 bytes]}}) = \color{green}{\checkmark}.$

However, the function stops at the first successful attempt, it assumed that the ciphertext $\texttt{{\color{gray}[14 bytes]}017b{\color{gray}[16 bytes]}}$ would decrypt to $\texttt{{\color{gray}[15 bytes]}01}$ , which is wrong. Thus it fails to recover the correct $m_1$ .

Notably, there are some message-ciphertext pairs that the hacker fails to handle, and one of them being $m_1 = \texttt{{\color{gray}[14 bytes]}0201}$ and $c_1 = \texttt{{\color{gray}[14 bytes]}01}c^*$ with $(c^* \oplus 3) < c^*$ .

Applying to the challenge

I used the username foo and password xxxxxxxx[02] ([02] is the byte with ASCII value 2). In that way, the plaintext would be username=foo&password=xxxxxxxx\x02, which is 31 bytes long and a [01] will be appended as a padding due to PKCS#7. We can generate ciphertexts repeatedly using the signin command until the ciphertext ends with 0102, 0103, 0106, …, 01fe, 01ff (all of them satisfy $c^* \oplus 3 < c^*$ ).

There are, in average, one out of 512 tokens that the hacker fails to decrypt.

How do we fix the attack script?

To handle the corner case, we need to check the plaintext so that it does not end with 0202, 030303 and so on. We will change the second last byte of $c_0$ to a different value. In that way, the second last byte of $m_1$ will be changed as well. If $m_1$ is still PKCS#7-compliant, then that means that $m_1$ ends with a 01. In the below figure, attempts #123+ and #124+ are the additional checks imposed.

Solution script

from pwn import *

r = remote('carbon-chal.firebird.sh', 36013)

r.sendline(b'register foo xxxxxxxx\x02')
# username=foo&password=xxxxxxxx\x02

tokens = []
while len(tokens) == 0:
    # Create 1024 tokens at once to save time
    for _ in range(1024):
        r.sendline(b'signin foo xxxxxxxx\x02')

    for _ in range(1024):
        r.recvuntil(b'Signed in as foo with token ')
        token = bytes.fromhex(r.recvuntil(b'.')[:-1].decode())
        
        if token[30] != 1: continue
        if token[31]^0x1^0x2 > token[31]: continue
        tokens.append(token.hex())

token = tokens[0]
print(f'{token = }')
r.sendline(f'hack {token}'.encode())
r.recvuntil(b'WHY? ')

r.interactive()

Threerider

? Who could ever expect that I am plagiarizing the same challenge twice?

Challenge Summary

The deadline for writing challenges is coming again!

Mystiz, who claimed himself not well-known reusing challenges, decided to free-ride and plagarize challenges from HKCERT CTF 2020. Uh, I mean, HKCERT CTF 2021. Maybe you can reuse the solve script last year for the flag.

Ciphertext:
f84bf7049cb55a0e1457d977e6cfbc0cc49ee1102da505e10aa3c32e619180446617ae2270cba3629b0851ae627236f19bb9cbfcadcd010eb923d170cbc2a7
Attachment: challenge.py

Suppose that the flag matches the regular expression firebird\{\w{53}\}. We define an encryption algorithm, $\mathcal{E}$ , with a 16-byte key $k_1k_2…k_{16}$ . Let $m$ be the message we would like to encrypt (all of the counters are set to zero):

Encrypt $m$ with AES-CTR using the key k1 00 00 00 ... 00 ( $k_1$ followed by 15 null bytes) and denote it by $t_1$ .
Encrypt $t_1$ with AES-CTR using the key k2 00 00 00 ... 00 and denote it by $t_2$ .
…
Encrypt $t_{15}$ with AES-CTR using the key k16 00 00 00 ... 00 and denote it by $t_{16}$ .
Return $t_{16}$ as the ciphertext.

$\mathcal{E}$ is used to encrypt the flag and we are given its ciphertext. The objective is to recover the flag. Notably, the challenge is highly referenced from Tenet and Tenet: The plagarism in HKCERT CTF 2020 and 2021 respectively.

Solution

FreeRider vs Threerider. We only know 133 bits of information. If we use the intended solution for FreeRider, there are at least

2^{123}

possible solutions and it is obviously infeasible to find the correct one in time.

We can borrow the idea from FreeRider. To get started, we can build a $133 \times 256$ matrix $A$ and a $133 \times 1$ matrix $b$ , with entries being 0 or 1:

$\left[\begin{matrix} b_{0, j_1} & b_{1, j_1} & b_{2, j_1} & … & b_{255, j_1} \\ b_{0, j_2} & b_{1, j_2} & b_{2, j_2} & … & b_{255, j_2} \\ && \vdots \\ b_{0, j_{133}} & b_{1, j_{133}} & b_{2, j_{133}} & … & b_{255, j_{133}} \\ \end{matrix}\right], b = \left[\begin{matrix} m_{j_1} + c_{j_1} \\ m_{j_2} + c_{j_2} \\ \vdots \\ m_{j_{133}} + c_{j_{133}} \end{matrix}\right]$

Similar to FreeRider, there is a $256 \times 1$ matrix $x$ such that $\cdot x = b\ (\text{mod}\ 2)$ . In particular, if $(x_0, x_1, …, x_{255})$ then $x_j = 1$ if and only if the byte $j$ occurs in the key for an odd number of times.

For example, if the key is 00 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d 0e 0e, then

$\begin{cases} x_j = 1 & \text{if}\ j = 0, 1, …, 13 \\ x_j = 0 & \text{otherwise} \end{cases}.$

It is remarkable that there are at most sixteen from $x_0, x_1, …, x_{255}$ such that $x_j = 1$ . For simplicity, let’s assume that there are exactly sixteen $x_j$ ’s such that $x_j = 1$ . In that case, if we pick $m$ entries $x_{j_1}, x_{j_2}, …, x_{j_m}$ randomly, then the probability of $x_{j_1} = x_{j_2} = … = x_{j_m} = 0$ would be

$\frac{240}{256} \cdot \frac{239}{255} \cdot … \cdot \frac{240-k+1}{256-k+1}.$

Since we have 133 equations and 256 unknowns, we will just randomly pick 123 $x_j$ ’s and assumed that to be zero. From above, the probability for them to actually be zero is around 1 in 56000.

Eventually, we can just repeatedly assume some of the unknowns to be zero and solve the equations. If there are less than 16 non-zero $x_j$ ’s, then that is very likely to be the vector we are looking for.

Solution script

import random
import re
from Crypto.Cipher import AES
from Crypto.Util import Counter
from operator import mul
from functools import reduce

#                      f i r e b i r d {                                                                                                           }
known = bytes.fromhex('ffffffffffffffffff8080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080808080ff')
m =     bytes.fromhex('66697265626972647b00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000007d')
c =     bytes.fromhex('f84bf7049cb55a0e1457d977e6cfbc0cc49ee1102da505e10aa3c32e619180446617ae2270cba3629b0851ae627236f19bb9cbfcadcd010eb923d170cbc2a7')

def xor(a, b):
    return bytes([u^^v for u, v in zip(a, b)])

keystreams = []
for k in range(256):
    cipher = AES.new(bytes([k]) + b'\0'*15, AES.MODE_CTR, counter=Counter.new(128, initial_value=int(0)))
    keystreams.append(
        cipher.encrypt(b'\0'*len(c))
    )

A = []
b = []

# The number of entries I guessed that they are zeroes
# Suggested: sampled_zeroes + number_of_equations >= 256 (or add some more to avoid less false positives...)

number_of_equations = bin(int.from_bytes(known, 'big')).count('1')
sampled_zeroes = 256 - number_of_equations
assert sampled_zeroes <= 256-16
print(f'{sampled_zeroes + number_of_equations = }')

for i, (rc, mc, cc) in enumerate(zip(known, m, c)):
    for j in range(8):
        if (rc>>j) & 1 == 0: continue
        mb = (mc>>j) & 1
        cb = (cc>>j) & 1

        row = [(k[i]>>j) & 1 for k in keystreams]

        A.append(row)
        b.append(mb^^cb)

F = GF(2)
A = Matrix(F, A)
b = vector(F, b)

hit_frequency = reduce(mul, [(256-16-k)/(256-k) for k in range(sampled_zeroes)])
print(f'{number_of_equations = }')
print(f'{sampled_zeroes = }')
print(f'Expecting a hit every {int(1/hit_frequency)} times')

attempt = 0
while True:
    attempt += 1

    # The 128 entries "I" guessed it is non-zero
    v = sorted(random.sample(range(256), k=256-sampled_zeroes))
    
    _A = A[:, v]
    try:
        x0 = _A.solve_right(b)
        for dx in _A.right_kernel():
            flag = c
            set_bits_count = 0
            for i in range(256-sampled_zeroes):
                if x0[i] == dx[i]: continue
                set_bits_count += 1
                flag = xor(flag, keystreams[v[i]])

            flag = flag.decode()
            if not re.match(r'firebird\{\w+\}', flag): continue
            if set_bits_count > 16: continue

            print(f'[*] Flag recovered at attempt #{attempt}: {flag}')
            assert False, 'done!'

    except KeyboardInterrupt:
        raise KeyboardInterrupt
    except AssertionError as err:
        raise err
    except:
        pass

Gabrielle de Micheli, Nadia Heninger (2020) “Recovering cryptographic keys from partial information, by example”
https://hal.science/hal-03045663/document ↩︎
Juliano Rizzo, Thai Duong (2010) “Practical Padding Oracle Attacks”
https://www.usenix.org/legacy/event/woot10/tech/full_papers/Rizzo.pdf ↩︎

Firebird Internal CTF 2023 Writeup

Randomsum

Challenge Summary

Solution

Solution script

Shelter

Challenge Summary

Solution

The padding oracle and its attacks

A corner case

Applying to the challenge

How do we fix the attack script?

Solution script

Threerider

Challenge Summary

Solution

Solution script

关于音频隐写的一些总结

2023西湖论剑web-writeup题解wp

相关文章

暂无评论

相关文章

Firebird Internal CTF 2023 Writeup

Randomsum

Challenge Summary

Solution

Solution script

Shelter

Challenge Summary

Solution

The padding oracle and its attacks

A corner case

Applying to the challenge

How do we fix the attack script?

Solution script

Threerider

Challenge Summary

Solution

Solution script

关于音频隐写的一些总结

2023西湖论剑web-writeup题解wp

相关文章

暂无评论

广告位

相关文章