HKCERT CTF 2022 Postmortem (I): Easier Crypto Challenges

This is the third year Black Bauhinia co-organized HKCERT CTF. This time I wrote nine challenges: Seven crypto, one reverse and one misc.

Similar to the last year, I have a series of three blog posts walking through the challenges that I wrote. We will discuss the four easier crypto challenges: Flawed ElGamal, Catch-22, Rogue Secret Assistant and Base64 encryption.

This is an index of the challenges I wrote for HKCERT CTF 2022. There are in total 309 teams participating:

1. Flawed ElGamal (Crypto; 127 solves)
2. Catch-22 (Crypto; 136 solves)
3. Base64 Encryption (Crypto; 6 solves)
4. Rogue Secret Assistant (Crypto; 7 solves)
5. Mystiz can’t code (Crypto; 1 solve)
6. Slow keystream (Crypto; 6 solves)
7. King of Rock, Paper, Scissors (Crypto; 1 solve)
8. Numbers go brrr (Reverse; 3 solves)
9. Minecraft Geoguessr (Misc; 4 solves)

海山樓 / Flawed ElGamal (Crypto)

Challenge Summary

Cryptography is difficult. It is hard to implement — every small mistakes would lead to a total break down.

I tried my very best to implement the ElGamal according to the Wikipedia page. What can go wrong?

The server will be returning an encrypted flag, (c1,c2)(c1​,c2​), every time a player connects to the server. This is the public key used:

p = 1444779821068309665607966047026245709114363505560724292470220924533941341173119282750461450104319554545087521581252757303050671443847680075401505584975539
g = 2
h = 679175474187312157096793918495021788380347146757928688295980599009809870413272456661249570962293053504169610388075260415234004679602069004959459298631976

Note that the ciphertext is computed by a flawed ElGamal such that (c1,c2)(c1​,c2​):

1. Generating a random $y\in [1,p-1]$,
2. Compute s:=hy mod ps:=hy mod p,
3. Compute c1:=gy mod pc1​:=gy mod p,
4. Compute c2:=m⋅sc2​:=m⋅s.

The goal is to obtain the flag, $m$.

Solution

An important observation is that c2:=m⋅sc2​:=m⋅s is not taken modulo $p$, therefore it is a multiple of $m$. If we get many ciphertexts (c1,c2)(c1​,c2​), (c1′,c2′)(c1′​,c2′​), … by connecting to the server multiple times, eventually we have

m=gcd⁡(c2,c2′,…).m=gcd(c2​,c2′​,...).

We can use the Euclidean algorithm to compute the GCD of two numbers, given below:

def gcd(a, b):
    while b != 0:
        a, b = b, a % b
    return a

To compute GCD of multiple numbers ($a,b,...,c$), we can apply GCD pairwise:

$$\gcd (a,b,...,c)=\gcd (...\gcd (\gcd (a,b),...),c).$$

After getting the number $m$, we can convert it into a string. From chall.py, the flag string is converted to a number by m = int.from_bytes(flag, 'big'). You may want to look at how a reverse operation can be done using int.to_bytes in Python. Eventually, we have hkcert22{4nd_th1s_t1m3_7h3_i5su3_1s_s0l31y_n0t_t4k1n9_m0du10s}.

九龍公園 / Catch-22 (Crypto)

Challenge Summary

You need a key to open the door… but what if the key is in the room?

We are given a web game. The player can navigate in the map and the goal is to access the flag.

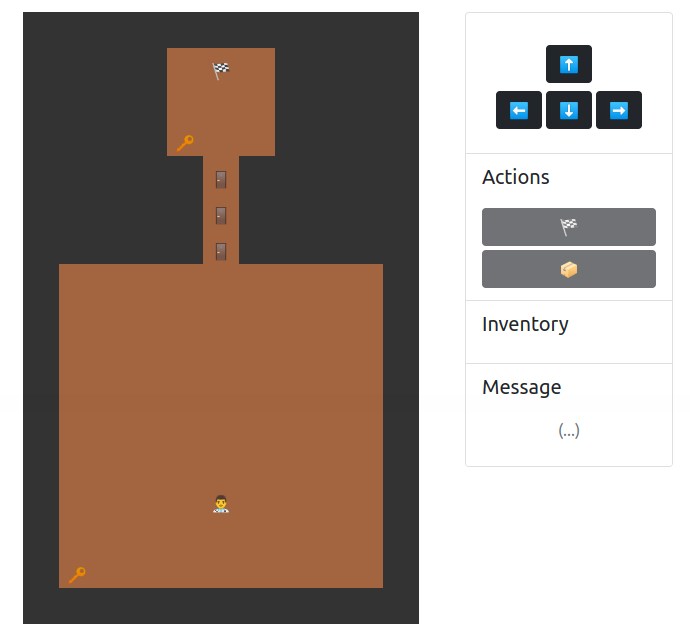
Notably, the game state (example given below) is encrypted by AES-ECB and is stored in the cookie.

{"username":"mystiz","x":13,"y":5,"inventory":[],"onMapItems":[{"item":0,"x":3,"y":4},{"item":0,"x":3,"y":4},{"item":1,"x":4,"y":5},{"item":1,"x":5,"y":5},{"item":1,"x":6,"y":5},{"item":0,"x":15,"y":1}]}

Solution

Part I: Interacting with the browser ?s

If you are using Google Chrome (probably the same for the common browsers), you can press F12 to open the developer tools and switch to the “Console” tab. You can read the cookies by typing the below snippet, and execute it by pressing Enter:

document.cookie

To set a cookie (for example, setting the value of the game-token to bar), type the below snippet and press Enter:

document.cookie="game-token=bar"

That’s it! You can manipulate cookies easily from your browser.

Part II: Encrypting messages of arbitrary length for block ciphers

Block ciphers are only capable to encrypt messages of a fixed length. For instance, Advanced Encryption Standard (AES) can only encrypt messages of 16 bytes. To encrypt messages of variable length, the messages are first padded such that their length is a multiple of the block size. After that, a mode of operation is picked.

The electronic codebook (ECB) mode of operation

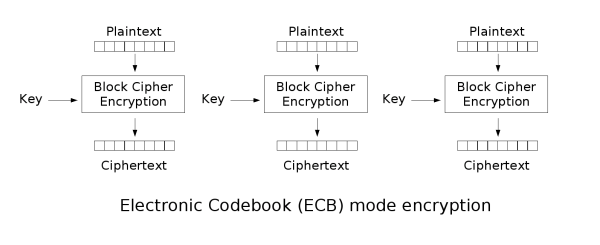
We are using ECB in this challenge. As illustrated above, the message blocks are encrypted independently. Sounds intuitive?

Let’s use a cookie as an example. It is encrypted in AES, which the block size is 16 bytes (equivalent to 32 hex characters):

fff21bf4a7d27a027502b1e1a253b35f071efbc3642eea3269d634e6c984feebf89e4736ab5ba5b4ef81b78a57a889ba4cf06024a9c302947c9a620592c23a76476e8424c54f1f47216f45d903c1baa4d2bd6f06d268a81b9d30326c80f521249fdba79cf386395248f82a0236c0771ae4210d738aa474035eda8131cc3f384ac551a93538d21903eb1b717741df7e1b7ac7350304f0d7f6db588f809cf319706f0a09ededf7547fab175c8e132a832c878303dd6064ba98361cf4f9784a0699

corresponds to the state

{"username":"mystiz_","x":13,"y":5,"inventory":[],"onMapItems":[{"item":0,"x":3,"y":4},{"item":1,"x":4,"y":5},{"item":1,"x":5,"y":5},{"item":1,"x":6,"y":5},{"item":0,"x":15,"y":1}]}

Let _ be the padding character (ASCII value 0x0b) according to PKCS5. These are the relations extracted between the plaintext and ciphertext blocks:

Part III: Casting the cut-and-paste attack

There is an interesting property for electronic codebook (ECB). Since the blocks are independently encrypted, no one would be able to identify if we swap two blocks. For instance, this is a message-ciphertext pair that we can forge (given the above relations):

Message:     {"username":"mys{"username":"mys
Ciphertext:  fff21bf4a7d27a027502b1e1a253b35f fff21bf4a7d27a027502b1e1a253b35f

This seemed to be useless, but we will use this idea to solve the challenge.

There are many ways to get the flag. My approach is to fill my inventory with keys. The inventory in the state is an array of item IDs. For instance, when there is two keys (ID = 0) in the inventory, the state would be {...,"inventory":[0,0],...}.

If we register an account called mys0,0,0,0,0,0,0,0 tiz_, then we have the corresponding token:

fff21bf4a7d27a027502b1e1a253b35ffb2333bf9573b1d240840aefb4f78b1e071efbc3642eea3269d634e6c984feebf89e4736ab5ba5b4ef81b78a57a889ba4cf06024a9c302947c9a620592c23a76476e8424c54f1f47216f45d903c1baa4d2bd6f06d268a81b9d30326c80f521249fdba79cf386395248f82a0236c0771ae4210d738aa474035eda8131cc3f384ac551a93538d21903eb1b717741df7e1b7ac7350304f0d7f6db588f809cf319706f0a09ededf7547fab175c8e132a832c878303dd6064ba98361cf4f9784a0699

If we move the second block between the fourth and the fifth blocks, then this is the new plaintext:

{"username":"mystiz_","x":13,"y":5,"inventory":[0,0,0,0,0,0,0,0 ],"onMapItems":[{"item":0,"x":3,"y":4},{"item":1,"x":4,"y":5},{"item":1,"x":5,"y":5},{"item":1,"x":6,"y":5},{"item":0,"x":15,"y":1}]}

We can concatenate the ciphertext blocks and update the cookie accordingly. Now we can fill our inventory with eight keys, which is more than enough! One last thing is to walk to the doors, unlock them with the keys and finally grab the flag! ?

hkcert22{cu7_4nd_p45t3_1ik3_4_3ng1n3er}

Final Words

There are a lot of possible ways to solve the challenge. These are some more weird game states that we crafted:

獅子山二號棒球場 / Base64 Encryption (Crypto)

Challenge Summary

People said that base64 is an encoding, not an encryption. Did they have a misconception about that?

If you believe that base64 is just an encoding, then convince me that you are able to “decode” the article (which is in English).

We are given an 1198-byte message (in English) encoded in base64, except that the charset is shuffled (without a mapping given). The goal is to recover the message.

Solution

Part I: Conservation of “characters” for substitution ciphers

In short, this is a substitution cipher to the character set A-Za-z0-9+/. Also, for substitution ciphers, each letter is encrypted into another letter.

For substitution ciphers, we can look at the frequencies for every character to recover the key. Say, if w appears the most in the ciphertext, it is probably encrypted from e because e is the most used letter in the English language. Can we apply the same to base64 encoded messages? Yes!

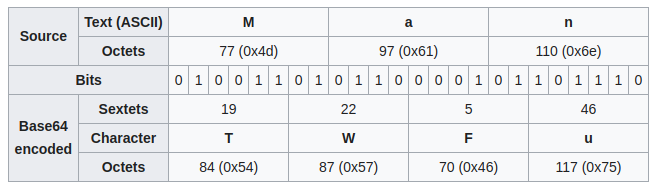
I will take t8.shakespeare.txt as the ground truth. To get started, I encoded it with base64 (the message begins with VGhpcyBpcyB0aGUgMTAwdGggRXRleHQgZmlsZSBwcmVzZ). After that, I partitioned the message into four groups, where group one contains the $4k+1$^th characters (i.e., VccaMd...) of the encoded message for $k\ge 0$; group two contains the $4k+2$^th characters (i.e., GyyGTG...); and so on.

Why four groups? This is because base64 encodes a message into strings with sizes being a multiple of 4. For instance, the $4k+1$^th encoded character comes from the six upper bits of the $3k+1$^th byte. Those characters always depend on the six most significant bits from the source bytes.

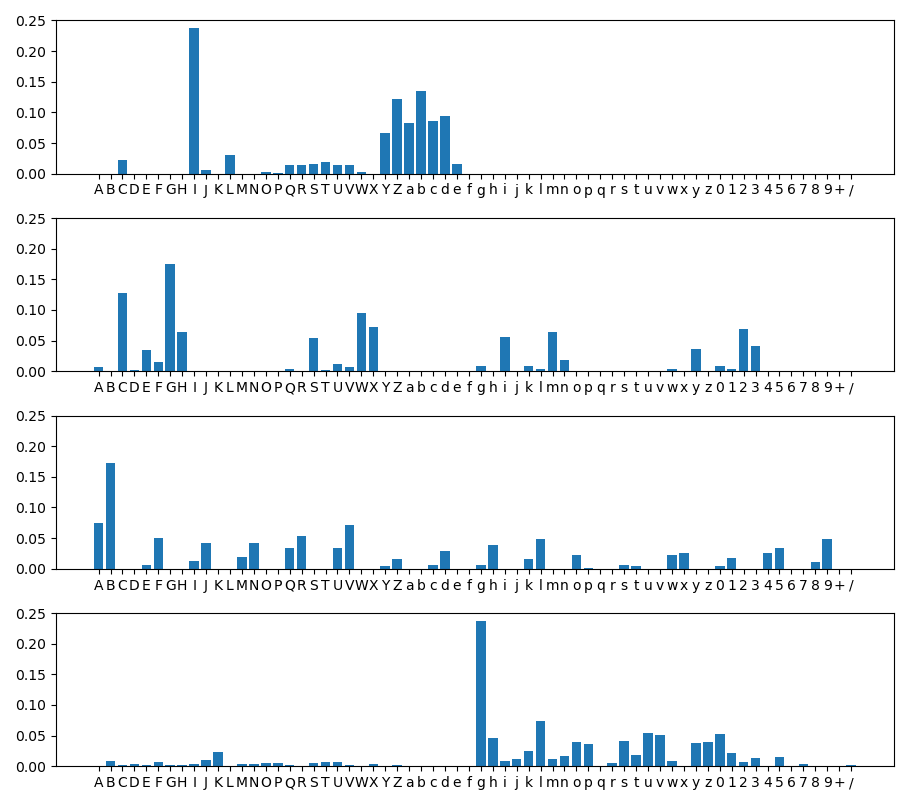
The bar charts are the distributions of the four groups. The distributions looked pretty different amongst these groups:

Part II: Frequency analysis – The first take

After that, we can look at the distribution of the ciphertexts. These are the ten most frequent characters in the ciphertext:

Why do we care about the most frequent characters? Well… who cares if you misspelt once in 1000 words. But it matters when you misspelt once every two words.

Anyway, let’s guess the character that encrypts to w. Maybe I? It appears the most from the base64-encoded Shakespeare’s text. Apparently not. The frequencies of I from the four groups are respectively 23.9%, 0.0%, 1.3% and 0.3%, which is not similar to the frequencies of encrypted w. Instead, it looks more like G, which has frequencies (0.0%, 17.6%, 0.0%, 2.1%).

We then continue to find the best guess that encrypts to Y. It is likely to be b, because the frequencies of the ciphertext Y and the plaintext b are respectively (18.5%, 0.0%, 1.0%, 0.0%) and (13.6%, 0.0%, 0.0%, 0.04%). Repeating the process, we have the plaintext-ciphertext mapping below:

Plaintext:  ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/
Ciphertext: 4czfHjwa9rl+Xds/1EbFuJioVRnYL0ym86UZ2WDMQPgBKGT5AN3Cqe7OShpvkxIt

“Decrypting” the ciphertext and decoding the whole message with base64, we have:

…which is not good at all.

Part III: Improving the heuristic

Since the article is written in English, it might be safe to assume that the ASCII code for all characters is in $[0,128)$. The most significant bit for each byte is zero. When encoded in base64, the below bits are zero:

• the first bit in group 1,
• the third bit in group 2, and
• the fifth bit in group 3.

What does it mean? We will never see ghijklmnopqrstuvwxyz0123456789+/ in group 1. Likewise, IJKLMNOPYZabcdefopqrstuv456789+/ and CDGHKLOPSTWXabefijmnqruvyz2367+/ will not appear in groups 2 and 3 respectively. To avoid those characters in the respective groups, we can add a huge penalty when those characters are picked.

Previously, we expected that Y decrypts to b as they have similar distributions. However, b will appear in group 3 and thus this is not a good choice. I may be a better corresponding plaintext in this case – the distributions are similar, and we are not penalised by picking it. Below are the new mapping and the plaintext:

Plaintext:  ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/
Ciphertext: 4czIHjwaYd8F1St/xEb7rJioV0+RLnygf6UGZWDMQPuBClqKAX35Te9ONhsv2mkp

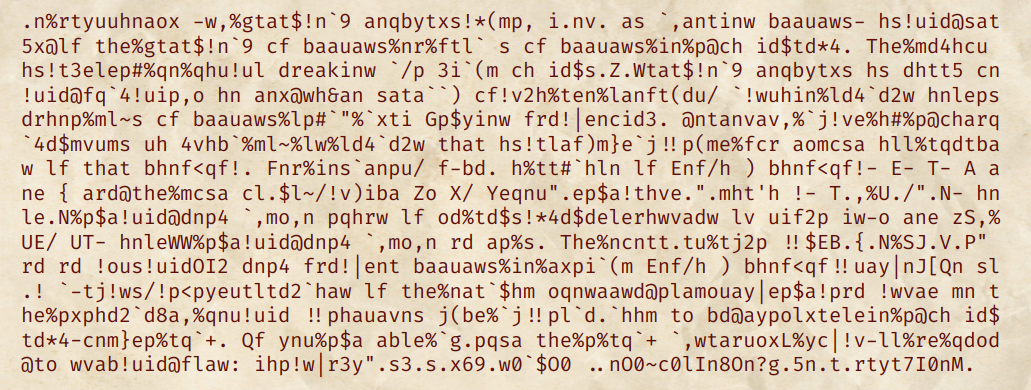
Part IV: Fine-tuning for the win

Although the article is still unreadable, we can read some words from it. There is a clear spelling mistake: Instead of that hs, it should instead be that is.

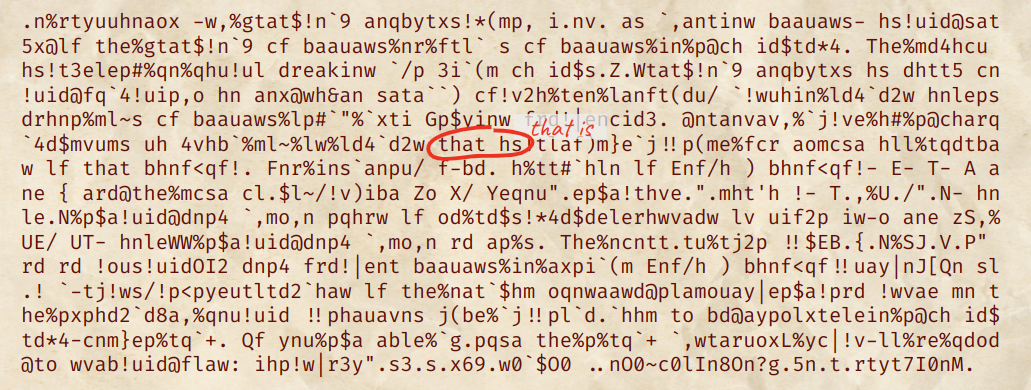
When encoded in base64, they are respectively ...aGF0IGhz... and ...aGF0IGlz.... Let’s make W and 6 decrypt to h and l respectively (they were corresponding to l and h). The article looked a bit better.

Plaintext:  ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/
Ciphertext: 4czIHjwaYd8F1St/xEb7rJioV0+RLnygfWUGZ6DMQPuBClqKAX35Te9ONhsv2mkp

We can fix the plaintext-ciphertext mapping by looking at the spelling mistakes. For instance, spaces should appear more frequently.

Eventually, it is quite manual work to recover the final message:

香港中文大學邵逸夫夫人樓 / Rogue Secret Assistant (Crypto)

Challenge Summary

Mystiz does not seem to give up using RSA to store his secrets. This time you are even allowed to send arbitrary public exponent, e. Can you unveil the secret flag?

When connected to the server, a 2048-bit RSA public exponent $n$ and a 128-character long secret are generated (none of them is given to the players). Players can send three different $e$ such that e≠1e=1. The message

The secret token is [SECRET] and it is encrypted with e = [E].

is encrypted using RSA with the key $(n,e)$. The goal is to recover the secret.

Solution

Part I: Connection of the unknowns by a congruence

Let m0m0​, m1m1​ and m2m2​ be the constant parts of the message, $s$ be the secret and ecec​ be the public exponent in ASCII (and $l$ be its length). Then the message would be

m:=256l+159⋅m0+256l+31⋅s+256l+1⋅m1+256⋅ec+m2.m:=256l+159⋅m0​+256l+31⋅s+256l+1⋅m1​+256⋅ec​+m2​.

Hereby the base message, m0m0​, m1m1​ and m2m2​, are constants given below:

# m0 = "The secret token is "
m0 = 0x5468652073656372657420746f6b656e2069732
# m1 = " and it is encrypted with e = "
m1 = 0x20616e6420697420697320656e6372797074656420776974682065203d20
# m2 = "."
m2 = 0x2e

You can imagine that m is a concatenation of The secret token is , followed by the secret,  and it is encrypted with e = , $e$ and a fullstop.

If we let further $c$ be the ciphertext of $m$, then c≡me (mod n)c≡me (mod n).

Since μl,e:=256l+159⋅m0+256l+1⋅m1+256⋅ec+m2μl,e​:=256l+159⋅m0​+256l+1⋅m1​+256⋅ec​+m2​ is known (we know $l$, m0m0​, m1m1​, m2m2​and ecec​), we will just use μl,eμl,e​ for simplicity. Connecting the two relations, we have the congruence

c≡(μl,e+256l+31⋅s)e (mod n).c≡(μl,e​+256l+31⋅s)e (mod n).

Now, how do we get $n$ and $s$ by sending three different $e$s (with e≠1e=1)? These are the congruences we have (the variables in red are unknown):

{c1=(μl1,e1+256l1+31⋅s)e1 (mod n)c2=(μl2,e2+256l2+31⋅s)e2 (mod n)c3=(μl3,e3+256l3+31⋅s)e3 (mod n)⎩⎪⎪⎪⎨⎪⎪⎪⎧​c1​=(μl1​,e1​​+256l1​+31⋅s)e1​ (mod n)c2​=(μl2​,e2​​+256l2​+31⋅s)e2​ (mod n)c3​=(μl3​,e3​​+256l3​+31⋅s)e3​ (mod n)​

Part II: Recovering the unknowns

Fortunately, $e$ does not need to be positive. We can set e1=−1e1​=−1 (i.e., l1=2l1​=2 because -1 is two-character long), then

c1=(μ2,−1+25633⋅s)−1 (mod n)⟹ (μ2,−1+25633⋅s)⋅c1=1 (mod n)⟹ s=1−μ2,−1⋅c125633⋅c1 (mod n)⟹ ⟹ ​c1​=(μ2,−1​+25633⋅s)−1 (mod n)(μ2,−1​+25633⋅s)⋅c1​=1 (mod n)s=25633⋅c1​1−μ2,−1​⋅c1​​ (mod n)​

Substitute the above congruence to the remaining two (assuming l2=l3=2l2​=l3​=2 for simplicity), then for $i=2,3$, we have:

ci≡(μ2,ei+25633⋅1−μ2,−1⋅c125633⋅c1)ei≡(μ2,ei+1−μ2,−1⋅c1c1)ei (mod n)⟹ ci−(μ2,ei+1−μ2,−1⋅c1c1)ei≡0 (mod n)⟹ ​ci​≡(μ2,ei​​+25633⋅25633⋅c1​1−μ2,−1​⋅c1​​)ei​≡(μ2,ei​​+c1​1−μ2,−1​⋅c1​​)ei​ (mod n)ci​−(μ2,ei​​+c1​1−μ2,−1​⋅c1​​)ei​≡0 (mod n)​

Thus we have two multiples of $n$. By taking its GCD, then we can recover $n$… but wait, how can we divide without the modulus? We can do multiplication instead. Now we assume further that e2=−2e2​=−2 and e3=−3e3​=−3. For $i=2,3$:

ci−(μ2,ei+1−μ2,−1⋅c1c1)ei≡0 (mod n)⟹ ci⋅(μ2,ei+1−μ2,−1⋅c1c1)−ei−1≡0 (mod n)⟹ ci⋅(μ2,ei+1−μ2,−1⋅c1c1)−ei⋅c1−ei−c1−ei≡0 (mod n)⟹ ci⋅(μ2,ei⋅c1+1−μ2,−1⋅c1)−ei−c1−ei≡0 (mod n)⟹ ⟹ ⟹ ​ci​−(μ2,ei​​+c1​1−μ2,−1​⋅c1​​)ei​≡0 (mod n)ci​⋅(μ2,ei​​+c1​1−μ2,−1​⋅c1​​)−ei​−1≡0 (mod n)ci​⋅(μ2,ei​​+c1​1−μ2,−1​⋅c1​​)−ei​⋅c1​−ei​−c1​−ei​≡0 (mod n)ci​⋅(μ2,ei​​⋅c1​+1−μ2,−1​⋅c1​)−ei​−c1​−ei​≡0 (mod n)​

Therefore, we have the two numbers

c2⋅(μ2,−2⋅c1+1−μ2,−1⋅c1)2−c12andc3⋅(μ2,−3⋅c1+1−μ2,−1⋅c1)3−c13,c2​⋅(μ2,−2​⋅c1​+1−μ2,−1​⋅c1​)2−c1​2andc3​⋅(μ2,−3​⋅c1​+1−μ2,−1​⋅c1​)3−c1​3,

which are both multiples of $n$. We can finally compute the GCD. Since the GCD of the two numbers are not necessarily equal to $n$ (it could be a small multiple of $n$), I attempted to remove small factors from the GCD in the solve script.

It is very unlikely that the n obtained is not equal to the actual public modulus. If that’s the case, we can simply re-run the script. Eventually, we will get the flag: hkcert22{r5a_i5_ju5t_a_6unch_0f_m4th5}.

Solve script

from math import gcd
from pwn import *

r = remote('chal.hkcert22.pwnable.hk', 28101)

def encrypt(e):
    r.sendline(str(e).encode())
    r.recvuntil(b'c = ')
    c = int(r.recvline().decode(), 16)
    return c

c1, c2, c3 = encrypt(-1), encrypt(-2), encrypt(-3)

µ1 = b'The secret token is ' + b'\0'*128 + b' and it is encrypted with e = -1.'
µ2 = b'The secret token is ' + b'\0'*128 + b' and it is encrypted with e = -2.'
µ3 = b'The secret token is ' + b'\0'*128 + b' and it is encrypted with e = -3.'

µ1, µ2, µ3 = [int.from_bytes(µ, 'big') for µ in [µ1, µ2, µ3]]

n = gcd(
    c2 * (µ2 * c1 + 1 - µ1 * c1)**2 - c1**2,
    c3 * (µ3 * c1 + 1 - µ1 * c1)**3 - c1**3
)
log.info(f'{n = }')

# Eliminate small factors
for k in range(2, 1000):
    while n % k == 0:
        n //= k

secret = pow(256, -33, n) * (pow(c1, -1, n) - µ1) % n
assert secret < 256**128
secret = int.to_bytes(secret, 128, 'big')
log.info(f'{secret = }')
r.sendline(secret)

r.interactive()