Metadata

I recently participated in LakeCTF by polygl0ts with NUS Greyhats and we got 5th place in the Quals.

We are also given the following description:

1
2
3

After getting hacked, the organizers of the CTF created a new and 
more secure account. You were able to intercept this PGP encrypted
e-mail. Can you decrypt it?

Aside: How PGP Works

PGP (Pretty Good Privacy) is an ancient (don’t kill me) encryption program that provides cryptographic privacy and authentication. There isn’t authentication in this challenge so I won’t be covering that.

In this challenge, the message is encrypted with RSA, one of the encryption schemes PGP supports, which is an asymmetric public-private key cryptosystem. In order to send somebody a message encrypted with RSA, the receiver has to expose a public key to everybody, but keep a private key secret. The sender would then encrypt the message with the receiver’s public key and send it over. The receiver will then use their private key, which nobody else but them knows, to decrypt the message. And so lies the theoretical security of RSA: You needthe private key in order to decrypt the message, it is theoretically computationally infeasible to do so without. Since only the receiver has their own private key, nobody can decrypt and read the message even if one were to intercept the encrypted message.

In the context of this challenge, ProtonMail exposes each accounts’s public key via their API https://api.protonmail.ch/pks/lookup?op=get&[email protected], and so we can get the public key of the intended recipient of the email in this challenge like so:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import requests
username = "epfl-ctf-admin2"
open("pub", "wb").write(requests.get(f"https://api.protonmail.ch/pks/lookup?op=get&search={username}@protonmail.com").content)
!cat pub | gpg --list-packets --verbose

# The relevant public key used for the challenge:

# :public sub key packet:
#     version 4, algo 1, created 1654083420, expires 0
#     pkey[0]: 
#         B1CF59A37A81DA7854EFFDB8C9FE9F2AABEC72FEC3D62324B24D9DB7DE01A3099F79E01219EC35DB4C58C
#         4C6A1B09865349E37B218F48CA9EC161AF84ED32AD5E7B096079DF567991C1B9E03A419B00D3FF6350849
#         C1E8C0753E2BCD54BDD33D81D5D564EE721A6BE80921B4CF220AA9F05F53D98106E59DE9ED327899FB633
#         86AB95F106E5CD60F4F578096B0E0C217928BE5CF6BBE10C6633F2DC320D224AEBF51FE34352738AD0B6E
#         0873C6C3DF5E49EF218F02688F1478D50A55A44D875BFC4799754C2F6135FF168C9C8E225EBF84850A01C
#         A7AE789D425824663FD2479ECC7AD71E1BE674FA59A42ACBAFA48EB43B181957145ED996739FFACE0A2F8
#         3432C0E9D64BCC5A68033AD8E7DF8191B1C0C157007544C8D1AE3A4B662D4B8FAE3549B2A63A076D62E34
#         847DD1AE307B3741A5CE1B5727A2586448FFFA1BB5FF019EA7230CC61DDDA1663B2E165322A02A13EF02B
#         9183704B083C3C7E9A9919C37693BE62A8B4F592041605AD046AC32D0DBFC0D312709D881DD164E2DD130
#         791BA70282FDBBA4391D78CD856AD237F73115DD1A0DD12EFE336E580C0B19C9A4B61F5119A0C1BAEC7C0
#         E313EB65C7405DE5B9BC4C6464A08547887F1C255C1E5ABE8989BF57D94C20E1B50151F4FA796EE46E69B
#         A77C289641EE560B80F2665BD8292C5DD25304BE9246E0FA38133DDD543FB26582DE80A8A0077A7ED636A
#         2DC3
#     pkey[1]: 010001
#     keyid: 2461439C55F8627A

Unfortunately for the entire world, RSA sucks ass. It is an incredibly brittle encryption scheme and just overall outdated and shitty. The intended solution for this challenge would involve exploiting a flaw in the public key to compute the private key (which should be computationally intractable!). More about that later.

For now I’ll be going through the Social Engineering Approach I took to solve this challenge.

Social Engineering Time

So I couldn’t find a flaw in the public key. The modulus is big (4096 bit) and can’t be factored as far as I tried. The exponent is the usual 0x10001. I also tried to look for the private key online, because sometimes private keys are compromised and floating somewhere in The World Wide Web, or for any flaws in the PGP configuration; are there any vulnerabilities in the versions used? All of these queries came up null.

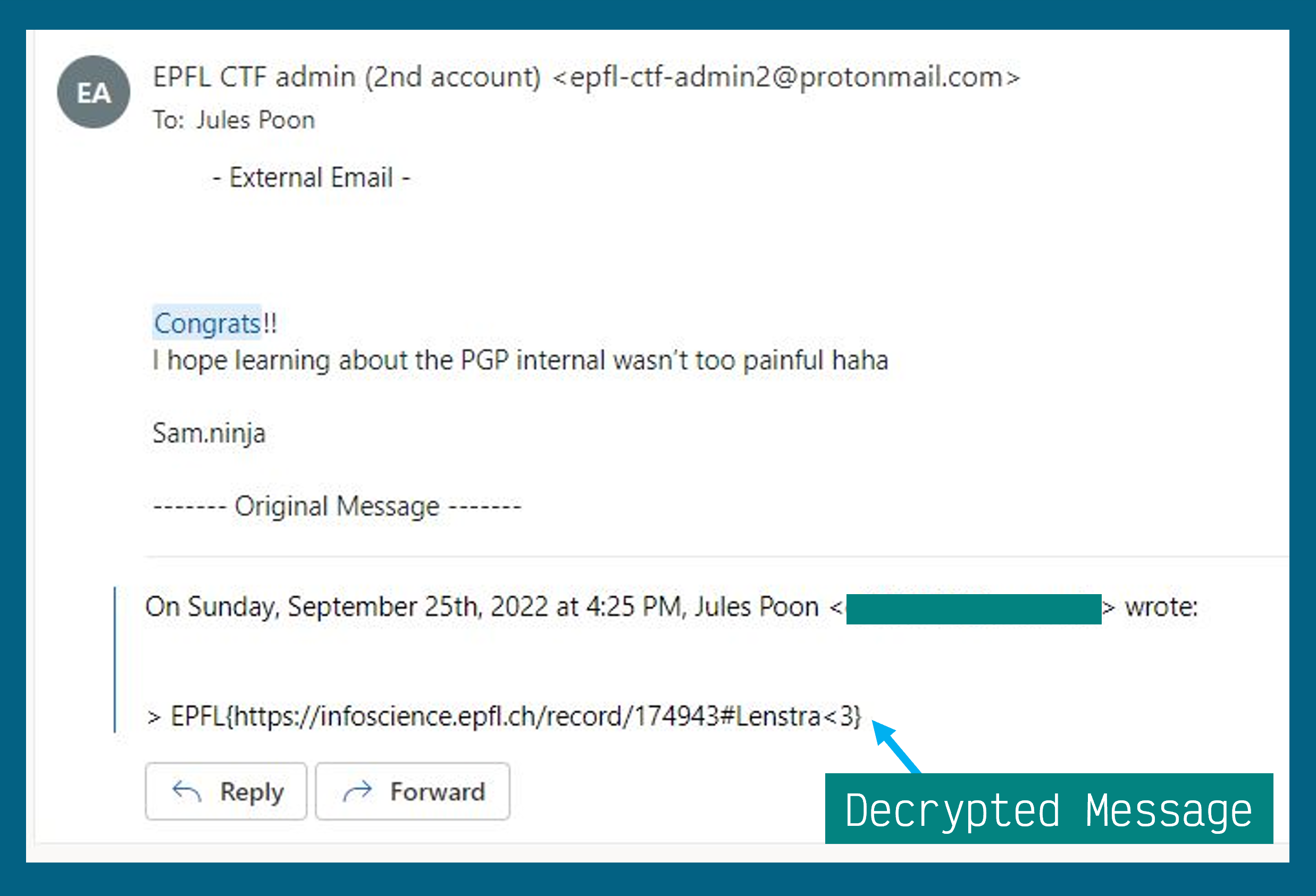
Three hours in, we were starting to get desperate, and so I tried this wild idea: Since the only person capable of decrypting the message is the one holding the private key (the intended recipient), what if we tricked the recipient to send us the decrypted message? Now look I totally didn’t expect this to work, but on the off chance it is actually somewhat the intended solution I gave it a go. Here’s how it works:

I send the intended recipient the encrypted email. ProtonMail would recieve the email, and since it’s not exactly good user interface to make the recipient manually decrypt each email they recieve, ProtonMail would decrypt the message and display the decrypted message to the recipient:

Now anybody who has used emails will know that typically the email client will append the entire conversation history to the reply email. ProtonMail, when sending the reply back to my email, will try to look for my PGP public key in order to re-encrypt the reply and the conversation history (which includes the decrypted message I want) to send it my way. Unfortunately, my email has no PGP public key for ProtonMail to use, so ProtonMail will just send the reply in plaintext, essentially tricking the organisers to decrypt the message for me:

Intended Solution

The intended recipient being [email protected] implies the existence of [email protected]. If you were to take the public keys of both accounts, you’d realise that the modulus (part of the public key) has a common factor. Taking gcd of both modulus, which is incredible fast, would allow you to recover the common factor and hence fully factor the intended recipient’s modulus. This allows one to compute the intended recipient’s private key and decrypt the message.